Lý thuyết Phân tích một số ra thừa số nguyên tố Toán 6 Cánh diều

I. Cách  tìm một ước nguyên tố của một số:

Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: Lần lượt làm phép chia n cho các số nguyên tố theo thứu tự tăng dần: 2;3;5;7;11;13;...

Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n

II.Phân tích một số ra thừa số nguyên tố

- Phân tích một số tự nhiên lớn hơn \(1\) ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

- Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

Sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

Ví dụ:

Phân tích số 12 ra thừa số nguyên tố bằng sơ đồ cây:

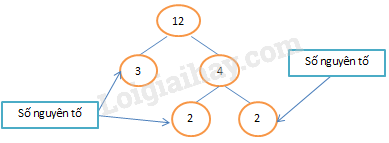
Như vậy \(12 = {2^2}.3\)

Sơ đồ cột:

Chia số \(n\) cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng  xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng \(1.\)

Ví dụ: Số \(76\) được phân tích như sau:

Như vậy \(76 = {2^2}.19\)

CÁC DẠNG TOÁN VỀ PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ

I. Phân tích các số cho trước ra thừa số nguyên tố

Phương pháp:

Ta thường phân tích một số tự nhiên $n\left( {n > 1} \right)$ ra thừa số nguyên tố bằng 2 cách:

+ Sơ đồ cây

+ Phân tích theo hàng dọc.

II. Ứng dụng phân tích một số ra thừa số nguyên tố để tìm các ước của số đó

Phương pháp:

+ Phân tích số cho trước ra thừa số nguyên tố.

+ Chú ý rằng nếu $c = a.b$  thì $a$  và $b$ là hai ước của $c.$

III. Bài toán đưa về việc phân tích một số ra thừa số nguyên tố

Phương pháp:

 Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố.

• Trả lời Hoạt động 1 trang 44 SGK Toán 6 Cánh Diều
• Luyện tập vận dụng 1 trang 44 SGK Toán 6 Cánh Diều
• Trả lời Hoạt động 2 trang 44 SGK Toán 6 Cánh Diều
• Trả lời Luyện tập vận dụng 2 trang 45 SGK Toán 6 Cánh Diều
• Trả lời Luyện tập vận dụng 3 trang 45 SGK Toán 6 Cánh Diều
• Giải Bài 1 trang 46 SGK Toán 6 Cánh Diều Tập 1
• Giải Bài 2 trang 46 SGK Toán 6 Cánh Diều Tập 1
• Giải Bài 3 trang 46 SGK Toán 6 Cánh Diều Tập 1
• Giải Bài 4 trang 46 SGK Toán 6 Cánh Diều Tập 1
• Giải Bài 5 trang 46 SGK Toán 6 Cánh Diều Tập 1