Giải bài 4.29 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác đều \(ABC\) có độ dài cạnh bằng 1.

a)      Gọi \(M\) là trung điểm của \(BC.\) Tính tích vô hướng của các cặp vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {BA} ,\) \(\overrightarrow {MA} \) và \(\overrightarrow {AC} .\)

b)     Gọi \(N\) là điểm đối xứng với \(B\) qua \(C.\) Tính tích vô hướng \(\overrightarrow {AM} .\overrightarrow {AN} \)

c)      Lấy điểm \(P\) thuộc đoạn \(AN\) sao cho \(AP = 3PN.\) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\,\,\overrightarrow {MP} \) thuộc hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} .\) Tính độ dài đoạn \(MP.\)

Lời giải chi tiết

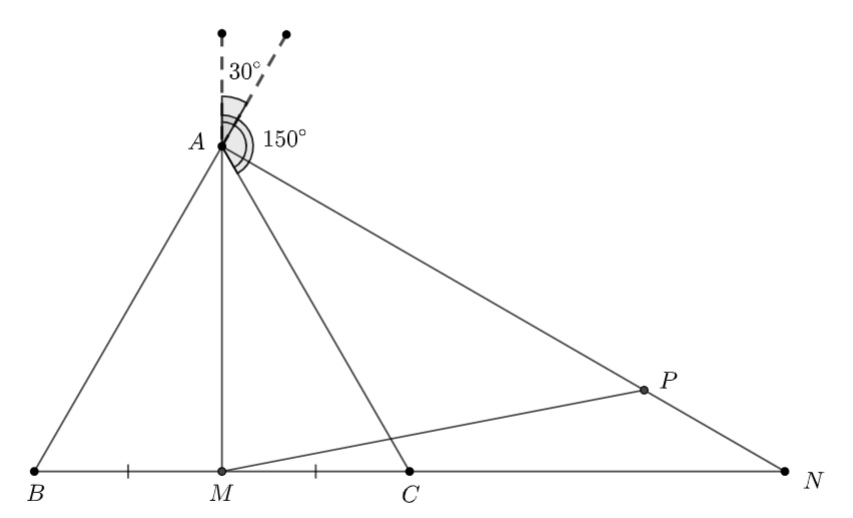
a) Xét \(\Delta ABC\) đều cạnh bằng 1 có: \(M\) là trung điểm của cạnh \(BC\)

\( \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{AM = \frac{{\sqrt 3 }}{2}}\\{\left( {\overrightarrow {MA} ,\overrightarrow {BA} } \right) = {{30}^ \circ }}\\{\left( {\overrightarrow {MA} ,\overrightarrow {AC} } \right) = {{150}^ \circ }}\end{array}} \right.\)

Ta có: \(\overrightarrow {MA} .\overrightarrow {BA}  = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {BA} } \right|.\cos \left( {\overrightarrow {MA} ,\overrightarrow {BA} } \right) = \frac{{\sqrt 3 }}{2}.\cos {30^ \circ } = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{3}{4}\)

\(\overrightarrow {MA} .\overrightarrow {AC}  = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {MA} ,\overrightarrow {AC} } \right) = \frac{{\sqrt 3 }}{2}.\cos {150^ \circ } = \frac{{\sqrt 3 }}{2}.\left( { - \frac{{\sqrt 3 }}{2}} \right) = \frac{{ - 3}}{4}\)

b) Ta có: \(MN = CM + CN = \frac{1}{2} + 1 = \frac{3}{2}\)

Ta có: \(\widehat {MAN} = {60^ \circ }\)

Xét \(\Delta AMN\) vuông tại \(M\) có:

\(AN = \sqrt {A{M^2} + M{N^2}}  = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{3}{2}} \right)}^2}}  = \sqrt 3 \)

Ta có: \(\overrightarrow {AM} .\overrightarrow {AN}  = \left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow {AN} } \right|.\cos \left( {\overrightarrow {AM} ,\overrightarrow {AN} } \right) = \frac{{\sqrt 3 }}{2}.\sqrt 3 .\cos {60^ \circ } = \frac{3}{2}.\frac{1}{2} = \frac{3}{4}\)

c) Ta có: \(P\) thuộc đoạn \(AN\) sao cho \(AP = 3PN.\)

Nên \(\overrightarrow {AP}  = \frac{3}{4}\overrightarrow {AN}  = \frac{3}{4}\left( {\overrightarrow {AC}  + \overrightarrow {CN} } \right) = \frac{3}{4}\left( {\overrightarrow {AC}  + \overrightarrow {BC} } \right) = \frac{3}{4}\left( {2\overrightarrow {AC}  - \overrightarrow {AB} } \right)\)

Ta có: \(\overrightarrow {MP}  = \overrightarrow {AP}  - \overrightarrow {AM}  = \frac{3}{4}\left( {2\overrightarrow {AC}  - \overrightarrow {AB} } \right) - \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \overrightarrow {AC}  - \frac{5}{4}\overrightarrow {AB} \)

Ta có: \(AP = \frac{3}{4}AN = \frac{{3\sqrt 3 }}{4}\)

\( \Rightarrow \) \(MP = \sqrt {A{P^2} + A{M^2} - 2AP.AM.\cos \widehat {MAP}}  = \frac{{\sqrt {21} }}{4}\)

• Giải bài 4.30 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.31 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.32 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.33 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.34 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.35 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.36 trang 66 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.37 trang 66 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
• Giải bài 4.38 trang 66 sách bài tập toán 10 - Kết nối tri thức với cuộc sống