Giải Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Đề bài

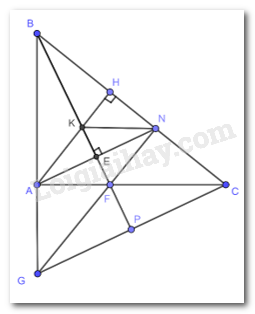
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\)(E ∈ AN).

a) Chứng minh rằng BE là tia phân giác của giác ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân. 

Lời giải chi tiết

a)      Xét \(\Delta BAE\)và\(\Delta BNE\) có :

BA = BN (giả thiết)

BF cạnh chung

\(\widehat {BEA} = \widehat {BEN}\)

\( \Rightarrow \Delta BAE = \Delta BNE\)(cạnh huyền-cạnh góc vuông)

\( \Rightarrow \widehat {ABF} = \widehat {NBF}\)(góc tương ứng)

\( \Rightarrow \) BE là phân giác của góc ABN

b)      Vì K là giao của 2 đường cao \( \Rightarrow \)K là trực tâm tam giác ABN

\( \Rightarrow \) KN vuông góc với AB(1)

Vì CA vuông góc với AB ( tam giác ABC vuông tại A)(2)

Từ (1) và (2) \( \Rightarrow \) KN song song với CA (quan hệ cùng vuông góc với 1 đường)

c)      Ta có \(\Delta BAF = \Delta BNF(c - g - c)\)do có :

\(\widehat {BEA} = \widehat {BEN}\)

BF cạnh chung

BN = BA

\( \Rightarrow \widehat {BNF} = \widehat {BAF}\)(2 góc tương ứng).

Mà \(\widehat {BAF} = 90^\circ \)

\( \Rightarrow \widehat {BNF} = \widehat {BAF} = {90^o}\)

\( \Rightarrow GN \bot BC\)

Ta có CA và GN là 2 đường cao của tam giác GBC

\( \Rightarrow \)F là trực tâm của tam giác GBC

\( \Rightarrow \)BF vuông góc với GC tại P

Xét \(\Delta BGP\)và\(\Delta BCP\)ta có :

BP cạnh chung

\(\widehat {BPC} = \widehat {BPG} = {90^o}\)

\(\widehat {PBC} = \widehat {PBG}\)

\( \Rightarrow \Delta BGP = \Delta BCP(c - g - c)\)

\( \Rightarrow BC = BG\)(2 cạnh tương ứng)

\( \Rightarrow \)Tam giác GBC cân tại B 

• Giải Bài 1 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 2 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 5 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 7 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 8 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
• Giải Bài 10 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo