Các dạng toán về khoảng cách

1. Bài toán tính khoảng cách từ một điểm đến một đường thẳng

Phương pháp:

Để tính khoảng cách từ điểm $M$ đến đường thẳng $\Delta $ ta cần xác định được hình chiếu $H$ của điểm $M$ trên đường thẳng $\Delta $, rồi xem $MH$ là đường cao của một tam giác nào đó để tính.

Điểm $H$ thường được dựng theo hai cách sau:

Cách 1: Trong $mp\left( {M,\Delta } \right)$ vẽ $MH \bot \Delta  \Rightarrow d\left( {M,\Delta } \right) = MH$

Cách 2: Dựng mặt phẳng $\left( \alpha  \right)$ qua $M$ và vuông góc với $\Delta $ tại $H$.

Khi đó $d\left( {M,\Delta } \right) = MH$.

2. Tính khoảng cách từ một điểm đến một mặt phẳng

Phương pháp:

Để tính được khoảng từ điểm $M$đến mặt phẳng $\left( \alpha  \right)$ thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm $M$ trên $\left( \alpha  \right)$.

TH1:

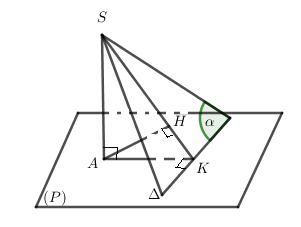
- Dựng \(AK \bot \Delta  \Rightarrow \Delta  \bot \left( {SAK} \right) \Rightarrow \left( \alpha  \right) \bot \left( {SAK} \right)\) và \(\left( \alpha  \right) \cap \left( {SAK} \right) = SK\).

- Dựng \(AH \bot SK \Rightarrow AH \bot \left( \alpha  \right) \Rightarrow d\left( {A,\left( \alpha  \right)} \right) = AH\)

TH2:

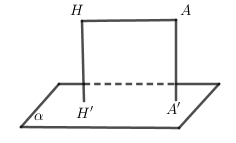
- Tìm điểm \(H \in \left( \alpha  \right)\) sao cho \(AH//\left( \alpha  \right) \Rightarrow d\left( {A,\left( \alpha  \right)} \right) = d\left( {H,\left( \alpha  \right)} \right)\)

TH3:

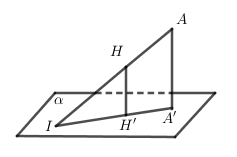
- Tìm điểm \(H\) sao cho \(AH \cap \left( \alpha  \right) = I\)

- Khi đó: \(\dfrac{{d\left( {A,\left( \alpha  \right)} \right)}}{{d\left( {H,\left( \alpha  \right)} \right)}} = \dfrac{{IA}}{{IH}} \Rightarrow {\rm{ }}d\left( {A,\left( \alpha  \right)} \right) = \dfrac{{IA}}{{IH}}.d\left( {H,\left( \alpha  \right)} \right){\rm{ }}\)

Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với tứ diện vuông (tương tư như hệ thức lượng trong tam giác vuông) là:

3. Phương pháp tính khoảng cách giữa hai đường thẳng

Phương pháp:

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:

+) Phương pháp 1: Dựng đoạn vuông góc chung $MN$ của $a$ và $b$, khi đó $d\left( {a,b} \right) = MN$.

Một số trường hợp hay gặp khi dựng đoạn vuông góc chung của hai đường thẳng chéo nhau:

Trường hợp 1: $\Delta $ và $\Delta '$ vừa chéo nhau vừa vuông góc với nhau

- Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta '$ và vuông góc với $\Delta $ tại $I$.

- Bước 2: Trong mặt phẳng $(\alpha )$ kẻ $IJ \bot \Delta '$.

Khi đó $IJ$ là đoạn vuông góc chung và $d(\Delta ,\Delta ') = IJ$.

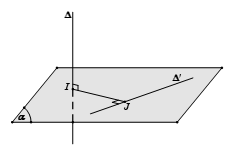
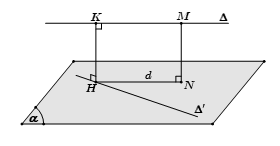
Trường hợp 2: $\Delta $ và $\Delta '$ chéo nhau mà không vuông góc với nhau

- Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta '$ và song song với $\Delta $.

- Bước 2: Dựng $d$ là hình chiếu vuông góc của $\Delta $ xuống $(\alpha )$ bằng cách lấy điểm $M \in \Delta $ dựng đoạn $MN \bot \left( \alpha  \right)$, lúc đó $d$ là đường thẳng đi qua $N$ và song song với $\Delta $.

- Bước 3: Gọi $H = d \cap \Delta '$, dựng $HK//MN$

Khi đó $HK$ là đoạn vuông góc chung và $d(\Delta ,\Delta ') = HK = MN$.

Hoặc

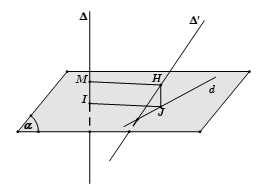
- Bước 1: Chọn mặt phẳng $(\alpha ) \bot \Delta $ tại $I$.

- Bước 2: Tìm hình chiếu $d$ của $\Delta '$ xuống mặt phẳng $(\alpha )$.

- Bước 3: Trong mặt phẳng $(\alpha )$, dựng $IJ \bot d$, từ $J$ dựng đường thẳng song song với $\Delta $ cắt $\Delta '$ tại $H$, từ $H$ dựng $HM//IJ$.

Khi đó $HM$ là đoạn vuông góc chung và $d(\Delta ,\Delta ') = HM = IJ$.

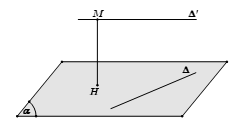
+) Phương pháp 2: Chọn mặt phẳng $(\alpha )$ chứa đường thẳng $\Delta $ và song song với $\Delta '$. Khi đó $d(\Delta ,\Delta ') = d(\Delta ',(\alpha ))$

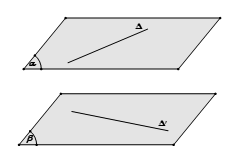
+) Phương pháp 3: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

+) Phương pháp 4: Sử dụng phương pháp vec tơ

a) $MN$ là đoạn vuông góc chung của $AB$ và $CD$ khi và chỉ khi $\left\{ \begin{array}{l}\overrightarrow {AM} = x\overrightarrow {AB} \\\overrightarrow {CN} = y\overrightarrow {CD} \\\overrightarrow {MN} .\overrightarrow {AB}  = 0\\\overrightarrow {MN} .\overrightarrow {CD}  = 0\end{array} \right.$

b) Nếu trong $\left( \alpha  \right)$ có hai vec tơ không cùng phương $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} $ thì $OH = d\left( {O,\left( \alpha  \right)} \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {OH}  \bot \overrightarrow {{u_1}} \\\overrightarrow {OH}  \bot \overrightarrow {{u_2}} \\H \in \left( \alpha  \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {OH} .\overrightarrow {{u_1}}  = 0\\\overrightarrow {OH} .\overrightarrow {{u_2}}  = 0\\H \in \left( \alpha  \right)\end{array} \right.$

• Câu hỏi 1 trang 115 SGK Hình học 11
• Câu hỏi 2 trang 115 SGK Hình học 11
• Câu hỏi 3 trang 116 SGK Hình học 11
• Câu hỏi 4 trang 116 SGK Hình học 11
• Câu hỏi 5 trang 116 SGK Hình học 11
• Câu hỏi 6 trang 118 SGK Hình học 11
• Bài 1 trang 119 SGK Hình học 11
• Bài 2 trang 119 SGK Hình học 11
• Bài 3 trang 119 SGK Hình học 11
• Bài 4 trang 119 SGK Hình học 11
• Bài 5 trang 119 SGK Hình học 11
• Bài 6 trang 119 SGK Hình học 11
• Bài 7 trang 120 SGK Hình học 11
• Bài 8 trang 120 SGK Hình học 11

• Lý thuyết khoảng cách