Bài 7 trang 111 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Trên đường tròn (O; R) lần lượt lấy ba điểm A, B, C theo thứ tự sao cho \(AB = R\sqrt 2 \) và sđ cung BC=30⁰.

a) Tính số đo của cung AB không chứa điểm C và tính độ dài dây AC theo R.

b) Từ A vẽ đường thẳng vuông góc với đường thẳng BC tại D. Tính độ dài các cung AD, DB, AB của đường tròn (ABD) theo R.

Lời giải chi tiết

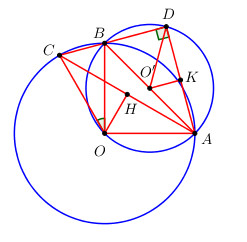
a) Xét tam giác OAB có : \(O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2} = A{B^2}\)

\( \Rightarrow \Delta OAB\) vuông tại O (định lí Pytago đảo)

\( \Rightarrow \widehat {AOB} = {90^0} = sdcung\,AB\) (số đo góc ở tâm bằng số đo cung bị chắn).

Mà \(sdcung\,BC = {30^0} \Rightarrow \widehat {BOC} = {30^0}\)(số đo góc ở tâm bằng số đo cung bị chắn).

\( \Rightarrow \widehat {AOC} = \widehat {AOB} + \widehat {BOC} = {90^0} + {30^0} = {120^0}\).

Gọi H là trung điểm của AC ta có \(OH \bot AC\) (quan hệ vuông góc giữa đường kính và dây cung).

Xét tam giác OAC có \(OA = OC = R \Rightarrow \Delta OAC\) cân tại O \( \Rightarrow OH\) là đường cao đồng thời là phân giác \( \Rightarrow \widehat {AOH} = \dfrac{1}{2}\widehat {AOC} = \dfrac{1}{2}{.120^0} = {60^0}\).

Xét tam giác vuông OAH có : \(AH = OA.\sin {60^0} = R.\dfrac{{\sqrt 3 }}{2}\)

\( \Rightarrow AC = 2AH = 2.R.\dfrac{{\sqrt 3 }}{2} = R\sqrt 3 \).

b) Tam giác ABD vuông tại D nên nội tiếp đường tròn đường kính AB, bán kính \(r = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 2 }}{2}\)

Xét tam giác OBC có \(OB = OC = R \Rightarrow \Delta OBC\) cân tại O

\( \Rightarrow \widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2} = \dfrac{{{{180}^0} - {{30}^0}}}{2} = {75^0}\)

Ta có : \(\widehat {OBD} + \widehat {OBC} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {OBD} = {180^0} - \widehat {OBC} = {180^0} - {75^0} = {105^0}\)

Tứ giác OADB có \(\widehat {AOB} + \widehat {ADB} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OADB là tứ giác nội tiếp

\( \Rightarrow \widehat {OAD} + \widehat {OBD} = {180^0}\) (tổng 2 góc đối của tứ giác nội tiếp)

\( \Rightarrow \widehat {OAD} = {180^0} - \widehat {OBD} = {180^0} - {105^0} = {75^0}\).

Mà \(\widehat {OAB} + \widehat {BAD} = \widehat {AOD} \)

\(\Rightarrow {45^0} + \widehat {BAD} = {75^0} \Rightarrow \widehat {BAD} = {30^0}\)

(do \(\Delta OAB\) vuông cân tại O nên \(\widehat {OAB} = \widehat {OBA} = {45^0}\))

Gọi O’ là trung điểm của AB.

Tam giác O’AD có \(O'A = O'D \Rightarrow \Delta O'AD\) cân tại O’

\( \Rightarrow \widehat {AO'D} = {180^0} - \widehat {O'AD} - \widehat {O'DA} \)\(\,= {180^0} - 2\widehat {O'AD} = {180^0} - {2.30^0} = {120^0}\)

\( \Rightarrow {l_{AD}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi .\dfrac{{R\sqrt 2 }}{2}.120}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{3}\)

Ta có \(\widehat {BO'D} + \widehat {AO'D} = {180^0}\) (kề bù) \( \Rightarrow \widehat {BO'D} = {180^0} - \widehat {AO'D} = {180^0} - {120^0} = {60^0}\)

\( \Rightarrow {l_{DB}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi .\dfrac{{R\sqrt 2 }}{2}.60}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{6}\)

\({l_{AB}} = \dfrac{{\pi rn}}{{180}} = \dfrac{{\pi \dfrac{{R\sqrt 2 }}{2}180}}{{180}} = \dfrac{{\pi R\sqrt 2 }}{2}\)

Xemloigiai.com

• Bài 1 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 2 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 3 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 4 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 5 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 6 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 8 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 9 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 10 trang 111 Tài liệu dạy – học Toán 9 tập 2
• Bài 11 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 12 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 13 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 14 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 15 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 16 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 17 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 18 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 19 trang 112 Tài liệu dạy – học Toán 9 tập 2
• Bài 20 trang 112 Tài liệu dạy – học Toán 9 tập 2