Bài 10 Trang 152 SGK Đại số và Giải tích 12 Nâng cao

Không tìm nguyên hàm hãy tính các tích phân sau:

LG a

\(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx} ;\)

Lời giải chi tiết:

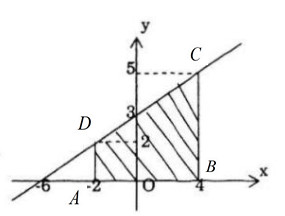
Vẽ đồ thị y=(x/2)+3, các đường thẳng \(x=-2,y=4\).

Tích phân cần tính là diện tích của hình phẳng giới hạn bởi đồ thị y=x/2+3, các đường thẳng x\-2, x=4 và trục hoành.

Tích phân đó bằng diện tích hình thang ABCD với AD=2, BC=5, AB=6.

Diện tích đó là \(\left( {2 + 5} \right){6 \over 2} = 21.\) 

Vậy \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx = 21} .\)

LG b

 \(\int\limits_{ - 1}^2 {\left| x \right|} dx\) 

Lời giải chi tiết:

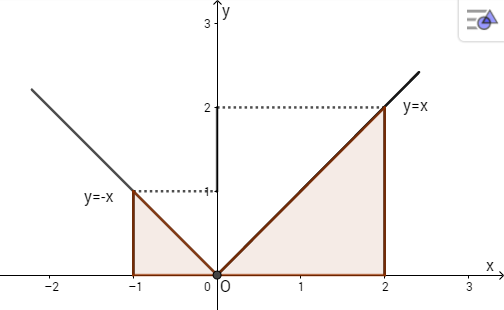
Vẽ đồ thị y=|x|

Diện tích hình phẳng giới hạn bởi y = |x|, trục hoành x = -1, x = 2 bằng tổng diện tích tam giác vuông tô màu.

Từ hình trên ta thấy hình A gồm 2 tam giác.

Do đó tích phân bằng diện tích của A và bằng:

\({1 \over 2}.1.1 + {1 \over 2}2.2 = 0,5 + 2 = 2,5\) 

Vậy \(\int\limits_{ - 1}^2 {\left| x \right|} dx = {5 \over 2}\).

LG c

\(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx\)

Phương pháp giải:

Áp dụng định lí 1.

Lời giải chi tiết:

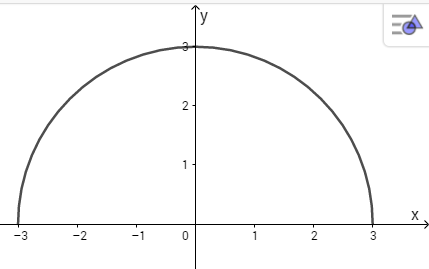
Vẽ nửa đường tròn \(x^2+y^2=9\).

Tích phân bằng diện tích nửa hình tròn \({x^2} + {y^2} = 9\)(hình).

Đây là đường tròn tâm là gốc tọa độ bán kính là R=3.

Do đó diện tích nửa hình tròn là \(\dfrac{1}{2}\pi {R^2} = \dfrac{1}{2}\pi {.3^2} = \dfrac{{9\pi }}{2}\)

Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx = 4,5\pi \)

Xemloigiai.com

• Bài 11 Trang 152 SGK Đại số và Giải tích 12 Nâng cao
• Bài 12 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
• Bài 13 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
• Bài 14 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
• Bài 15 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
• Bài 16 Trang 153 SGK Đại số và Giải tích 12 Nâng cao