Giải bài 4 trang 18 SGK Hình học 12

Cho hình bát diện đều \(ABCDEF\) 

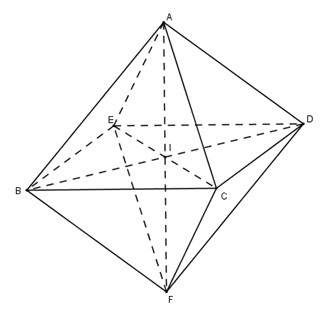
Chứng minh rằng :

LG a

a) Các đoạn thẳng \(AF, BD\) và \(CE\) đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.

Phương pháp giải:

+) Sử dụng tính chất của mặt phẳng trung trực.

+) Dấu hiệu nhân biết hình vuông: Hình thoi có hai đường chéo bằng nhau là hình vuông.

Lời giải chi tiết:

a) Do \(B, C, D, E\) cách đều \(A\) và \(F\) nên chúng đồng phẳng (cùng thuộc mặt phẳng trung trực của \(AF\)).

Tương tự, \(A, B, F, D\) đồng phẳng và \(A, C, F, E\) đồng phẳng.

Gọi \(I\) là giao của \((AF)\) với \((BCDE)\). Khi đó \(B, I, D\) là những điểm chung của hai mặt phẳng \((BCDE)\) và \((ABFD)\) nên chúng thẳng hàng. Tương tự, \(E, I , C\) thẳng hàng.

Vậy \(AF, BD, CE\) đồng quy tại \(I\).

Vì \(BCDE\) là hình thoi nên \(EC\) vuông góc với \(BC\) và cắt \(BC\) tại \(I\) là trung điểm của mỗi đường. \(I\) là trung điểm của \(AF\) và \(AF\) vuông góc với \(BD\) và \(EC\), do đó các đoạn thẳng \(AF, BD\), và \(CE\) đôi một vuông góc với nhau cắt nhau tại trung điểm của chúng.

Cách khác:

Giả sử bát diện đều \(ABCDEF\) có cạnh bằng \(a.\)

\(B, C, D, E\) cách đều \(A\) và \(F\) suy ra \(B, C, D, E\) cùng nằm trên mặt phẳng trung trực của đoạn thẳng \(AF\)

Trong mp \((BCDE)\), ta có \(BC = CD = DE = EB (= a)\)

\(⇒ BCDE\) là hình thoi

\(⇒ BD ⊥ EC\) và \(BD, EC\) cắt nhau tại trung điểm mỗi đường.

Chứng minh tương tự ta suy ra \(AF\) và \(BD, AF\) và \(CE\) vuông góc nhau và cắt nhau tại trung điểm mỗi đường.

LG b

b) \(ABFD, AEFC\) và \(BCDE\) là những hình vuông.

Phương pháp giải:

+) Sử dụng tính chất của mặt phẳng trung trực.

+) Dấu hiệu nhân biết hình vuông: Hình thoi có hai đường chéo bằng nhau là hình vuông.

Lời giải chi tiết:

b) Ta có tứ giác \(DCBE\) là hình thoi.

Do \(AI\) vuông góc \((BCDE)\) và \(AB = AC =AD = AE\) nên \(IB = IC= ID = IE\).

Từ đó suy ra hình thoi \(BCDE\) là hình vuông. Tương tự \(ABFD, AEFC\) là những hình vuông.

Cách khác:

Gọi trung điểm \(BD, CE, AF là O\).

\(\begin{array}{l}BO \bot AO \Rightarrow AB = \sqrt {A{O^2} + B{O^2}} \\AO \bot OE \Rightarrow AE = \sqrt {A{O^2} + O{E^2}} \end{array}\)

Mà \(AB = AE (= a) ⇒ BO = OE ⇒ BD = EC\)

⇒ Hình thoi \(BCDE\) là hình vuông.

Chứng minh tương tự: \(ABFD, AEFC\) đều là hình vuông.

Xemloigiai.com

• Trả lời câu hỏi 1 trang 15 SGK Hình học 12
• Trả lời câu hỏi 2 trang 16 SGK Hình học 12
• Trả lời câu hỏi 3 trang 17 SGK Hình học 12
• Trả lời câu hỏi 4 trang 18 SGK Hình học 12
• Giải bài 1 trang 18 SGK Hình học 12
• Giải bài 2 trang 18 SGK Hình học 12
• Giải bài 3 trang 18 SGK Hình học 12

• Lý thuyết khối đa diện lồi và khối đa diện đều