Đề kiểm tra 45 phút - Đề số 6 - Chương 1 - Hình học 9

Đề bài

Bài 1. Tính giá trị của biểu thức :

\(A = {{3\cot 77^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ  + {{\cos }^2}64^\circ  - {{\cos }^2}71^\circ  - {{\cos }^2}19^\circ } \over {{{\sin }^2}34^\circ  + {{\sin }^2}56^\circ  + {{\sin }^2}15^\circ  + {{\sin }^2}75^\circ }}\)

Bài 2. Cho hình thang ABCD (AB // CD) có \(AB = 1cm\), \(CD = 5cm\) và \(\widehat C = 30^\circ ,\widehat D = 60^\circ \). Tính diện tích hình thang ABCD.

Bài 3. Cho tam giác ABC có ba góc nhọn, các đường cao BI, CK cắt nhau tại H. Trên đoạn HB, HC lần lượt lấy các điểm D và E sao cho \(\widehat {ADC} = \widehat {AEB} = 90^\circ .\)

a. Chứng minh rằng ∆ADE cân 

b. Cho \(AD = 6cm, AC = 10cm\). Tính DC, CI và diện tích \(∆ADI.\)

LG bài 1

Phương pháp giải:

Sử dụng:

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

\({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

Lời giải chi tiết:

Ta có: 

\(\eqalign{   A &= {{3\cot 77^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ  + {{\cos }^2}64^\circ  - {{\cos }^2}71^\circ  - {{\cos }^2}19^\circ } \over {{{\sin }^2}34^\circ  + {{\sin }^2}56^\circ  + {{\sin }^2}15^\circ  + {{\sin }^2}75^\circ }}  \cr  &  = {{3\tan 13^\circ } \over {2\tan 13^\circ }} - {{{{\cos }^2}26^\circ  + {{\sin }^2}26^\circ  - {{\cos }^2}71^\circ  - {{\sin }^2}71^\circ } \over {{{\sin }^2}34^\circ  + {{\cos }^2}34^\circ  + {{\sin }^2}15^\circ  + {{\cos }^2}15^\circ }}  \cr  &  = {3 \over 2} - {{1 - \left( {{{\cos }^2}71^\circ  + {{\sin }^2}71^\circ } \right)} \over {1 + 1}}\cr& = {3 \over 2} - {{1 - 1} \over 2} = {3 \over 2} \cr} \)

LG bài 2

Phương pháp giải:

* Trong một tam giác vuông, mỗi cạnh góc vuông bằng: 

+) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

+) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

 * Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

Lời giải chi tiết:

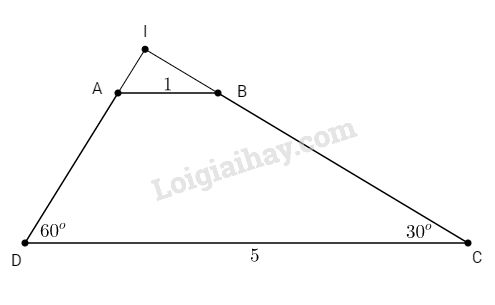
Gọi I là giao điểm của CB và DA

Khi đó ∆ICD vuông tại I (vì \(\widehat C + \widehat D = 30^\circ  + 60^\circ  = 90^\circ \)) và \(ID = {1 \over 2}CD\) (trong tam giác vuông cạnh đối diện góc 30˚ bằng nửa cạnh huyền).

Mặt khác ∆ICD vuông tại I, ta có:

\(IC = CD.\sin D = 5.\sin 60^\circ  = {{5\sqrt 3 } \over 2}\,\left( {cm} \right)\)

Do đó: \({S_{ICD}} = {1 \over 2}IC.ID = {1 \over 2}.{{5\sqrt 3 } \over 2}.{5 \over 2} = {{25\sqrt 3 } \over 8}\,\left( {c{m^2}} \right)\)

Vì AB // CD (gt) nên:

\(\widehat {IAB} = \widehat D = 60^\circ \) (đồng vị)

và \(\widehat {IBA} = \widehat C = 30^\circ \)

Tương tự, trong ∆IAB vuông tại I, ta có:

\(\eqalign{  & IA = AB.\sin 30^\circ  = 1.\sin 30^\circ  = {1 \over 2}\,\left( {cm} \right)  \cr  & va\,IB = AB.\cos 30^\circ  = 1.\cos 30^\circ  = {{\sqrt 3 } \over 2}\,\left( {cm} \right) \cr} \)

Do đó: \({S_{IAB}} = {1 \over 2}IA.IB = {1 \over 2}.{1 \over 2}.{{\sqrt 3 } \over 2} = {{\sqrt 3 } \over 8}\,\left( {c{m^2}} \right)\)

Ta có: \({S_{ABCD}} = {S_{ICD}} - {S_{IAB}} \)\(\;= {{25\sqrt 3 } \over 8} - {{\sqrt 3 } \over 8} = {{24\sqrt 3 } \over 8} = 3\sqrt 3 \,\left( {c{m^2}} \right)\)

LG bài 3

Phương pháp giải:

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau: 

+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\) 

+) \(H{A^2} = HB.HC\) 

+) \(AB.AC = BC.AH\)

+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago). 

Lời giải chi tiết:

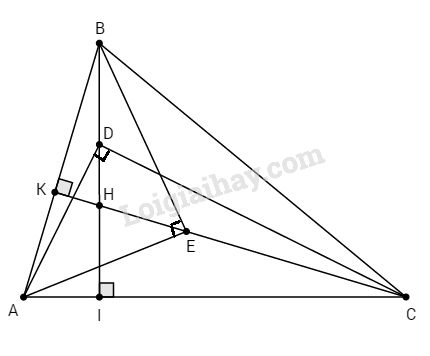
a. Ta có: ∆ADC vuông tại D, đường cao DI nên : 

\(A{D^2} = AC.AI\) (định lí 1) (1)

Tương tự: ∆AEB có đường cao EK:

\(A{E^2} = AB.AK\) (2)

Dễ thấy ∆AIB đồng dạng ∆AKC (g.g)

\(\eqalign{  &  \Rightarrow {{AB} \over {AC}} = {{AI} \over {AK}}  \cr  &  \Rightarrow AB.AK = AC.AI\,\left( 3 \right) \cr} \)

Từ (1), (2) và (3) \( \Rightarrow A{D^2} = A{E^2}\)

Vậy ∆ADE cân tại E.

b. Ta có: ∆ADC vuông :

\(DC = \sqrt {A{C^2} - A{D^2}}  = \sqrt {{{10}^2} - {6^2}}  = 8\,\left( {cm} \right)\)

Lại có DI là đường cao của tam giác vuông ADC, ta có:

\(C{D^2} = CA.CI\) (định lí 1)

\( \Rightarrow CI = {{C{D^2}} \over {CA}} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)\)

Do đó: \(AI = AC – CI = 10 – 6,4 = 3,6 (cm)\)

Ta có: \(DI.CA = DA.DC\) (định lí 3)

\( \Rightarrow DI = {{DA.DC} \over {AC}} = {{6.8} \over {10}} = 4,8\,\left( {cm} \right)\)

Vậy \({S_{ADI}} = {1 \over 2}AI.DI = {1 \over 2}.3,6.4,8 = 8,64\,\left( {c{m^2}} \right)\)

Xemloigiai.com

• Đề kiểm tra 45 phút - Đề số 1 - Chương 1 - Hình học 9
• Đề kiểm tra 45 phút - Đề số 2 - Chương 1 - Hình học 9
• Đề kiểm tra 45 phút - Đề số 3 - Chương 1 - Hình học 9
• Đề kiểm tra 45 phút - Đề số 4- Chương 1 - Hình học 9
• Đề kiểm tra 45 phút - Đề số 5 - Chương 1 - Hình học 9
• Đề kiểm tra 45 phút - Đề số 7 - Chương 1 - Hình học 9