Bài 8 trang 176 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác DEF cân tại D. Gọi M là trung điểm của DE, N là trung điểm của DF.

a) Chứng minh rằng EN = FM.

b) Gọi K là giao điểm của EN với FM. Chưng sminh rằng tam giác KEF cân.

c) Chứng minh rằng DK là phân giác \(\widehat {EDF}\)

d) DK cắt EF tại H. Biết DE = 10 cm, EF = 12 cm. Tính DH.

Lời giải chi tiết

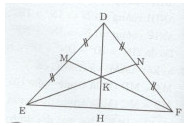
a)Ta có: \(DM = ME = {{DE} \over 2}\)   (M là trung điểm của DE)

\(DN = NF = {{DF} \over 2}\)   (N là trung điểm của DF)

Mà DE = DF (tam giác DEF cân tại D)

Do đó: DM = ME = DN = NF.

Xét tam giác DEN và DFM ta có:

DN = DM (chứng minh trên)

\(\widehat {EDN} = \widehat {FDN}\)   (góc chung)

DE = DF (tam giác DEF cân tại D)

Do đó: \(\Delta DEN = \Delta DFM(c.g.c) \Rightarrow EN = FM.\)

b) Ta có: \(\widehat {DEF} = \widehat {DFE}(\Delta DEF\)  cân tại D) \(\Rightarrow \widehat {DEN} + \widehat {KEF} = \widehat {DFM} + \widehat {KFE}\)

Mà \(\widehat {DEN} = \widehat {DFM}(\Delta DEN = \Delta DFM)\)  . Do đó: \(\widehat {KEF} = \widehat {KFE}.\)

Vậy tam giác KEF cân tại K.

c) Xét tam giác DEK và DFK ta có:

DE = DF (tam giác DEF cân tại D)

\(\widehat {DEK} = \widehat {DFK}(\Delta DEN = \Delta DFM)\)

EK = FK (chứng minh câu b)

Do đó: \(\Delta DEK = \Delta DFK(c.g.c) \Rightarrow \widehat {EDK} = \widehat {FDK}.\)

Vậy DK là tia phân giác của góc EDF.

d) Xét tam giác DHE và DHF ta có:

DH là cạnh chung

DE = DF (tam giác DEF cân tại D)

\(\widehat {EDH} = \widehat {FDH}\)   (chứng minh câu c)

Do đó: \(\Delta DHE = \Delta DHF(c.g.c) \Rightarrow \widehat {DHE} = \widehat {DHF}\)

Mà \(\widehat {DHE} + \widehat {DHF} = {180^0}\)   (kề bù)

Nên \(\widehat {DHE} + \widehat {DHE} = {180^0} \Rightarrow 2\widehat {DHE} = {180^0} \Rightarrow \widehat {DHE} = {90^0}.\)

Ta có: \(EH = HF = {{EF} \over 2} = {{12} \over 2} = 6cm(\Delta DHE = \Delta DHF)\)

Tam giác HDE vuông tại H:

\(D{E^2} = D{H^2} + E{H^2}\)   (định lí Pythagore)

Do đó: \(D{H^2} = D{E^2} - E{H^2} = {10^2} - {6^2} = 100 - 36 = 64\)

Mà DH > 0. Vậy \(DH = \sqrt {64}  = 8(cm).\)

Xemloigiai.com

• Bài 1 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 2 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 3 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 4 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 5 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 6 trang 175 Tài liệu dạy – học Toán 7 tập 1
• Bài 7 trang 176 Tài liệu dạy – học Toán 7 tập 1
• Bài 9 trang 176 Tài liệu dạy – học Toán 7 tập 1
• Bài 10 trang 176 Tài liệu dạy – học Toán 7 tập 1