Giải mục 1 trang 21, 22, 23 SGK Toán 10 tập 1 - Chân trời sáng tạo

HĐ Khởi động

Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm

Phương pháp giải:

Phân biệt các miền trong hình chữ nhật

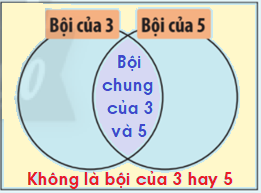
Lời giải chi tiết:

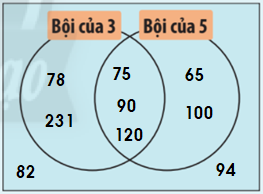
Bội của 3: 75, 78, 90, 120, 231

Bội của 5: 65, 75, 90, 100, 120

Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.

Không là bội của 3 và không là bội của 5: 82, 94

HĐ Khám phá 1

Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):

a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.

b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.

c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Lời giải chi tiết:

a) Tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn là:

\(A = \{ {a_1};{a_2};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)

Tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ là:

\(B = \{ {a_1};{a_3};{a_5};{a_6};{a_8};{a_{10}}\} \)

b) Tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ là:

\(C = \{ {a_1};{a_5};{a_6};{a_8};{a_{10}}\} \)

c) Tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ là:

\(D = \{ {a_1};{a_2};{a_3};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)

Thực hành 1

Xác định các tập hợp \(A \cup B\) và \(A \cap B\), biết:

a) \(A = \{ a;b;c;d;e\} \), \(B = \{ a;e;i;u\} \)

b) \(A = \{ x \in \mathbb{R}|\;{x^2} + 2x - 3 = 0\} \),\(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \)

Phương pháp giải:

\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)

\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)

Lời giải chi tiết:

a) \(A \cup B = \{ a;b;c;d;e;i;u\} \), \(A \cap B = \{ a;e\} \)

b) Phương trình \({x^2} + 2x - 3 = 0\) có hai nghiệm là 1 và -3, nên \(A = \{ 1; - 3\} \)

Phương trình \(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \) có hai nghiệm là 1 và -1, nên \(B = \{ 1; - 1\} \)

Từ đó, \(A \cup B = \{ 1; - 1; - 3\} \), \(A \cap B = \{ 1\} .\)

Thực hành 2

Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)

Hãy xác định \(A \cap B\).

Phương pháp giải:

\(A \cap B = \{ (x;y)|(x;y) \in A\) và \((x;y) \in B\} \)

Lời giải chi tiết:

a) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},3x - y = 9,x - y = 1\} \)

Tức là \(A \cap B\)là tập hợp các cặp số (x;y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 9\\x - y = 1\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y = 3x - 9\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 3x - 9\\y = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 8\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\end{array}\)

Vậy \(A \cap B = \{ (4;3)\} .\)

Vận dụng

Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?

Phương pháp giải:

Kí hiệu A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Sử dụng biểu đồ Ven, minh họa tập hợp các khán giả đã tham gia bình chọn (\(A \cup B\)) và các khán giả không tham gia bình chọn.

Lời giải chi tiết:

Gọi A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Theo giả thiết, \(n(A) = 85,n(B) = 72,n(A \cap B) = 60\)

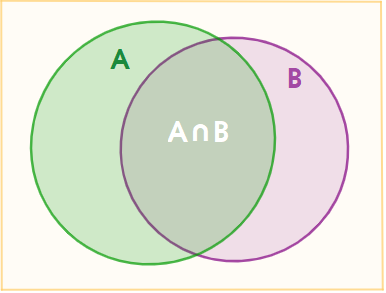
Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số khán giả đã tham gia bình chọn, nhưng số khán giả bình chọn cho cả hai thí sinh được tính hai lần. Do đó, số khán giả đã tham gia bình chọn là:

\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 85 + 72 - 60 = 97\)

Như vậy trong hội trường 100 khán giả, có 97 khán giải đã tham gia bình chọn, còn lại số khán giả không tham gia bình chọn là: \(100 - 97 = 3\) (khán giả).

• Giải mục 2 trang 23, 24, 25 SGK Toán 10 tập 1 - Chân trời sáng tạo
• Giải bài 1 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo
• Giải bài 2 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo
• Giải bài 3 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo
• Giải bài 4 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo
• Giải bài 5 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo
• Giải bài 6 trang 25 SGK Toán 10 tập 1 – Chân trời sáng tạo

• Lý thuyết Các phép toán trên tập hợp - SGK Toán 10 Chân trời sáng tạo