Giải bài 9.35 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức

Đề bài

Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.

a) Chúng minh \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\)

Gợi ý: Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).

b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\).

Lời giải chi tiết

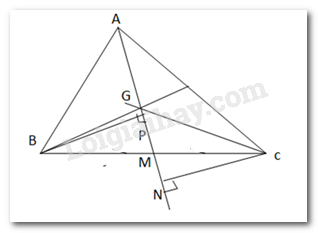
a)

Kẻ  \(BP \bot AM\), \(CN \bot AM\)

Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng

minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).

b)

-Chứng minh \({S_{GAB}} = {S_{GAC}}\)

-Sử dụng \({S_{ABC}} = {S_{GAB}} + {S_{GAC}} + {S_{GBC}}\)

Lời giải

a) Vì G là trọng tâm tam giác ABC nên \(GM = \dfrac{1}{3}AM\)

Kẻ \(BP \bot AM\) ta có

 \(\begin{array}{l}{S_{GMP}} = \dfrac{1}{2}BP.GM\\{S_{ABM}} = \dfrac{1}{2}BP.AM\end{array}\)

\( \Rightarrow \dfrac{{{S_{GMP}}}}{{{S_{ABM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMP}} = \dfrac{1}{3}{S_{ABM}}\)(1)                         

Tương tự, kẻ \(CN \bot AM\), ta có  

\(\begin{array}{l}{S_{GMC}} = \dfrac{1}{2}CN.GM\\{S_{ACM}} = \dfrac{1}{2}CN.AM\\ \Rightarrow \dfrac{{{S_{GMC}}}}{{{S_{ACM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)\end{array}\)

Cộng 2 vế của (1) và (2) ta có: 

\(\begin{array}{l}{S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \Rightarrow {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\end{array}\)

b) 

Ta có

\(\begin{array}{l}{S_{GAB}} = \dfrac{1}{2}BP.AG\\{S_{GAC}} = \dfrac{1}{2}CN.AG\end{array}\)

Xét \(\Delta BPM\) và \(\Delta CNM\) có:

\(\widehat {BPM} = \widehat {CNM} = {90^0}\)

 BM = CM ( M là trung điểm của BC)

\(\widehat {PMB} = \widehat {CMN}\)(2 góc đối đỉnh)

\( \Rightarrow \Delta BPM = \Delta CNM\)(cạnh huyền – góc nhọn)

\( \Rightarrow \) BP = CN (cạnh tương ứng)

\( \Rightarrow {S_{GAB}} = {S_{GAC}}\)

Ta có: \(AG = \dfrac{2}{3}AM\)

\(\begin{array}{l}{S_{ACB}} = {S_{GAB}} + {S_{GAC}} + {S_{GCB}}\\ \Rightarrow {S_{ACB}} = {S_{GAB}} + {S_{GAC}} + \dfrac{1}{3}{S_{ABC}}\\ \Rightarrow \dfrac{2}{3}{S_{ABC}} = 2{S_{GAC}}\\ \Rightarrow \dfrac{1}{3}{S_{ABC}} = {S_{GAC}} = {S_{GAB}}\end{array}\)

• Giải bài 9.31 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức
• Giải bài 9.32 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức
• Giải bài 9.33 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức
• Giải bài 9.34 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức